連関図とは?(新QC7つ道具の手法解説②)



連関図法とは
連関図法は、新QC7つ道具のうちの1で、原因と結果が複雑に絡み合った問題に対して用いる手法です。
連関図の作成を進めることで、原因と結果を1つひとつ解きほぐしていきます。
連関図法を用いることで、多くの原因が関わり、どう手をつけてよいか分からない問題に対して、原因を紐解き整理することができ、広い視野で全体を見渡すことができるようになります。
そして、的確に真因を掴むことができるようになるのです。
新QC7つ道具に関しては、下記ページで詳細を解説しています。
[reg-bnr]新QC7つ道具の活用シーン 新QC7つ道具、通称N7(エヌナナ) 新QC7つ道具とは、数値化できない言語データを整理し、新たな発想を得て問題解決へつなげる手法です。 略してN7(読み:エヌナナ)と呼ばれま...
連関図の作成手順
連関図は、次の5STEPで作成・活用を進めていきます。
STEP1.取り上げる問題を決める
STEP2.一次要因を抽出する
STEP3.要因を掘り下げる
STEP4.主要因を抽出する
STEP5.活用方法を決める
連関図作成のポイント
連関図は、事実を元に作成していきましょう。
意識するポイントは、下記が挙げられます。
・実際に現場で問題点を探しながら作成すること
・実際の作業者をメンバーに加えること
・数値データを取れるものは数値データを用いること
・写真やグラフを併せて載せること
複雑な問題になればなるほど、事実を1つ1つ明らかにしながら紐解いていくことが重要です。事実とは異なる推測が混じることで誤った結論を導いてしまわないよう注意しましょう。
メンバーの認識を合わせにも
メンバーの認識を合わせることにも活用しましょう。
起こっている問題の背景にどんな要因が隠れているのか、現場では事実としてどのようなことが起こっているのかを関係者で話し合うことで、メンバーの認識を合わせることができます。
それにより、メンバー全員が正確な現場の状況を把握することができ、より現場に即した取り組みを行えるようになり、他のメンバーとの連携も行いやすくなります。連関図を作成することで、「個人の頭が整理され、問題に対する理解が深まる」という効果だけでなく、「チームの活動の質が高まる」という効果もあるのです。積極的に活用していきましょう。
こんな時には連関図を使おう
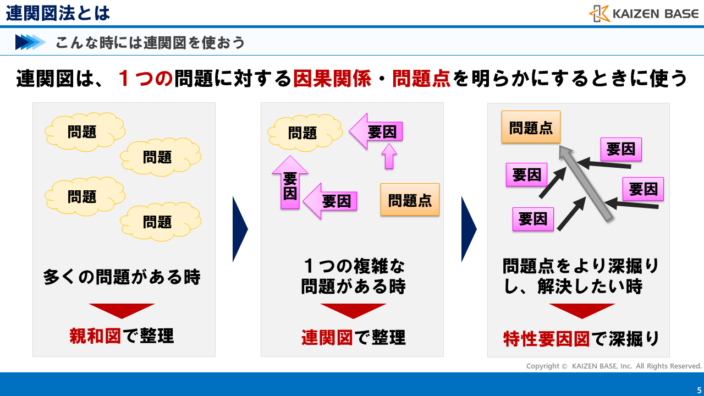
連関図は、1つの問題に対する要因の因果関係や問題点を明らかにするときに使います。
1つの複雑な問題がある時に、連関図を活用して因果関係や問題点を整理するのです。
このように多くの問題がある時には、第2章で学んだ親和図を用いて整理します。
明確な問題点に対し、より深掘りして解決したい時には、QC7つ道具の1つ、特性要因図を用います。
まずは多くの問題を親和図を用いて整理し、ターゲットとなった問題に対して連関図法を用いる。
そして、連関図法により明らかになった問題点に対し、特性要因図を用いて深掘りし解決を図る、という使い方をすると効果的ですね。


「連関図」に関する教材ダウンロード
無料会員に登録すると教材のダウンロードができます!
ダウンロードした資料につきましては、コンテンツ利用規約に同意の上、ご利用くださいますようお願い致します。例えば、下記の行為は禁止となります(利用規約を一部抜粋)
- 本コンテンツを利用してのコンサルティング業務をする行為
- 利益享受または販売を目的として利用(販売やWEBサイトへの掲載等)をする行為
- 二次的著作物を制作し第三者に配布する行為
- 弊社または第三者の財産、名誉、プライバシー等を侵害する行為
| 使用用途 | 社内教育や発表資料作成における作業効率化等 |
|---|---|
| ファイル形式 | PowerPoint |
| 教材ダウンロード | 無料会員に登録すると、ココにダウンロードボタンが表示されます。 |
ログイン/無料会員登録はこちらから
無料会員の方はログインしてください。
新規会員登録のご案内
会員登録特典!
- 閲覧できる動画が2倍に増加
- カイゼン講座で使用している資料の一部がダウンロード可能
- 実務で使えるテンプレートがダウンロード可能
- カイゼン情報や限定情報満載のメルマガが受け取れる
個人向け有料動画サービスに申し込むと、さらに充実!
限定の学習動画が閲覧可能になります!
関連学習動画
-
k-019
新たな発想を生み出す!新QC7つ道具の使い方

有料サービス限定
5:マトリックス図法とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- マトリックス図法とは
- マトリックス図の作成手順
- マトリックス図作成のポイント
- 系統図と組み合わせて活用する
- まとめ
-
k-019
新たな発想を生み出す!新QC7つ道具の使い方

有料サービス限定
8:マトリックス・データ解析とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- マトリックス・データ解析とは
- マトリックス・データ解析の考え方
- マトリックス・データ解析の解析手順
- まとめ
-
k-019
新たな発想を生み出す!新QC7つ道具の使い方

無料会員限定
2:親和図法とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- 親和図法とは
- 親和図の作成方法
- 親和図作成のポイント
- こんな時には親和図を使おう
- 親和図の作成により生まれる効果
- まとめ
-
k-019
新たな発想を生み出す!新QC7つ道具の使い方

有料サービス限定
4:系統図法とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- 系統図法とは
- 系統図の作成手順
- 系統図作成のポイント
- 親和図、連関図との違い
- まとめ
-
k-019
新たな発想を生み出す!新QC7つ道具の使い方

公開講座
1:新QC7つ道具とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- 新QC7つ道具とは
- 言語データとは
- 新QC7つ道具の活用のポイント
- まとめ
-
k-019
新たな発想を生み出す!新QC7つ道具の使い方

有料サービス限定
6:アローダイヤグラム法とは
受講対象者
生産部門全般(新入社員/一般)- カリキュラム構成
-
- アローダイヤグラム法とは
- アローダイヤグラムの作成手順
- アローダイヤグラム作成のポイント
- 進捗管理のポイント
- まとめ